笛子 声学:从振动原理到乐器实践

人如何感受到声音
声音模型
物体通过周期性的振动使介质(空气)振动形成声波,$1\,\mathrm{s}$ 内振动的次数为频率值。单频声波可简化为正弦行波,方程如下:
\begin{align} y(x,t) = A \cdot \sin(kx - \omega t + \phi_0) \end{align}
$ y(x,t) $ 表示介质质点的位移。在介质同一点,$y$ 是 $t$ 的函数;在同一时间,$y$ 是 $x$ 的函数。
$A$ 为振幅,决定声音响度;
$k$ 为角波数,$λ$ 为波长,$f$ 为频率,$v$ 为波速, $k = 2π / λ$,$λ=v/f$,$k$ 反映了在 $2π$ 弧度的相位变化内,波在空间上重复了多少次;
$ω$ 为角频率,$ω = 2πf$,它反映了在 $2π$ 弧度的相位变化内,波在时间上重复了多少次;
$x$ 为空间位置,表示沿着波传播方向的位置坐标;
$t$ 为观测时刻;
$ϕ_0$ 为初相位,描述单频波时可简化为 $0$。
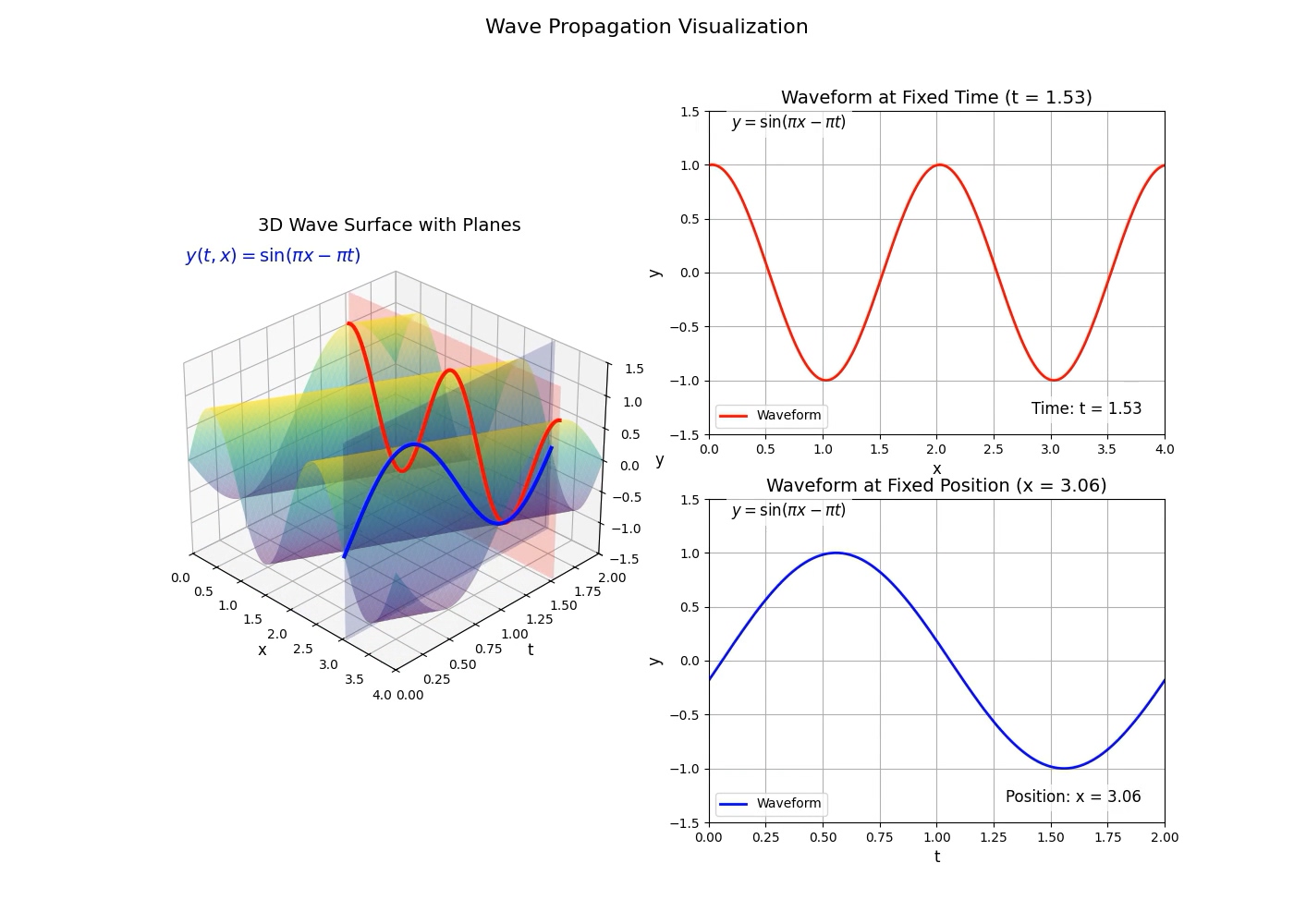
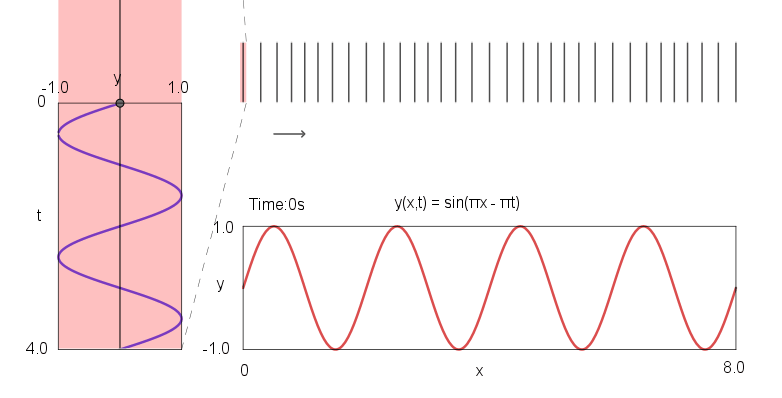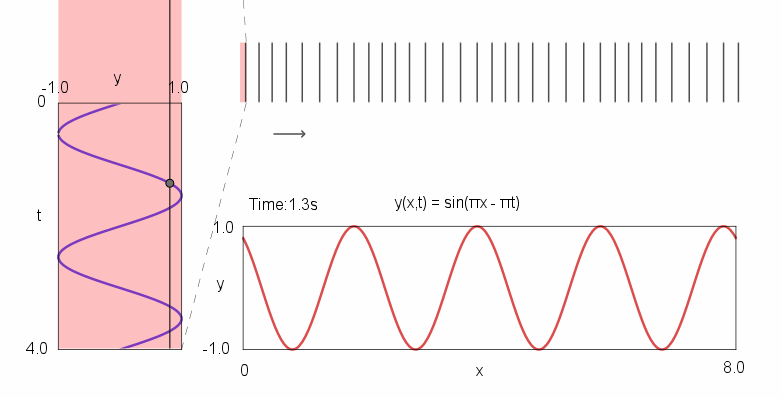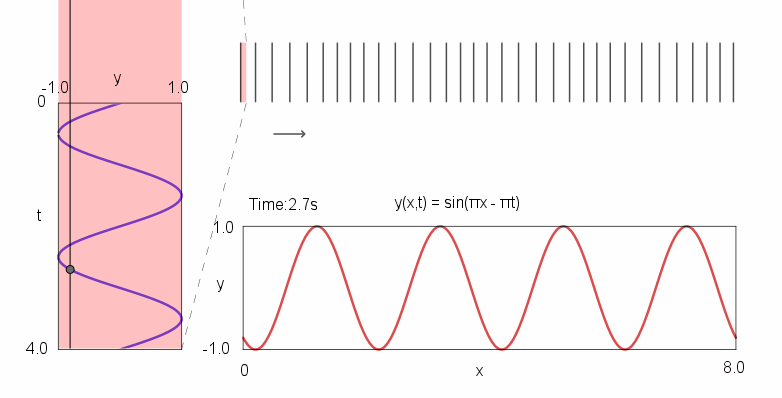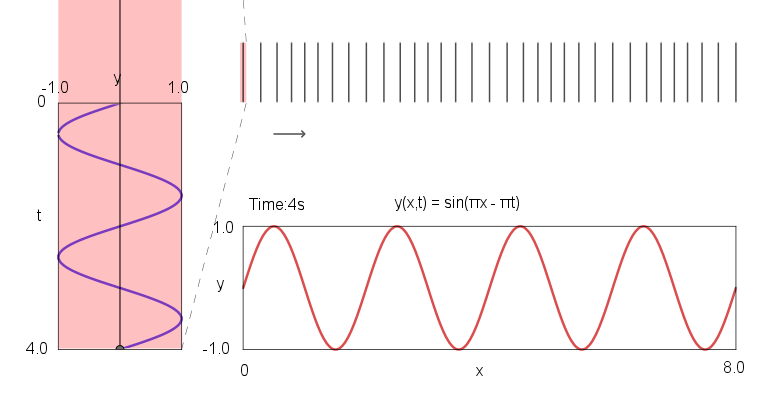
如图,在 $(x,t,y)$ 三维坐标系中绘制行波方程 $y(x,t)= \sin(πx - πt )$ 的波动曲面、代表固定时刻的平面 $t = \text{Time}$、代表固定位置的平面 $x = \text{Position}$、波动曲面与平面 $t = \text{Time}$ 的交线(即时刻 $\text{Time}$ 的空间波形 $y(x, \text{Time})$)、以及波动曲面与平面 $x = \text{Position}$ 的交线(即位置 $\text{Position}$ 的时间历程 $y(\text{Position}, t)$)。通过此三维可视化,可以清晰地观察到行波的传播过程、特定时刻的空间波形分布以及特定位置点的振动历史。
下图为声波方程的动态示意图,竖线“|”表示空气粒子。
音的频率
频率 $f$ 是表示声音高低的物理量,单位 $\mathrm{s}^{-1}$ ,记为 $\mathrm{Hz}$。频率小则音调低,频率大则音调高,人耳能感知的频率范围为 $20 \sim 20\,000 \,\mathrm{Hz}$。 声波方程用 $f$ 表示可写为
\begin{align} y(x,t) = A \sin\left(2\pi f \left(\frac{x}{v} - t\right) + \phi_0\right) \end{align}
两个不同频率的声波的动态示意图如下:
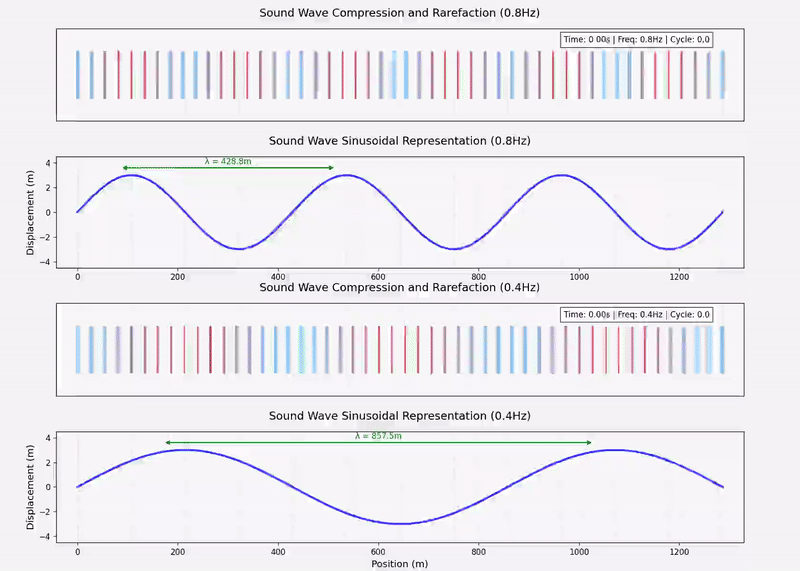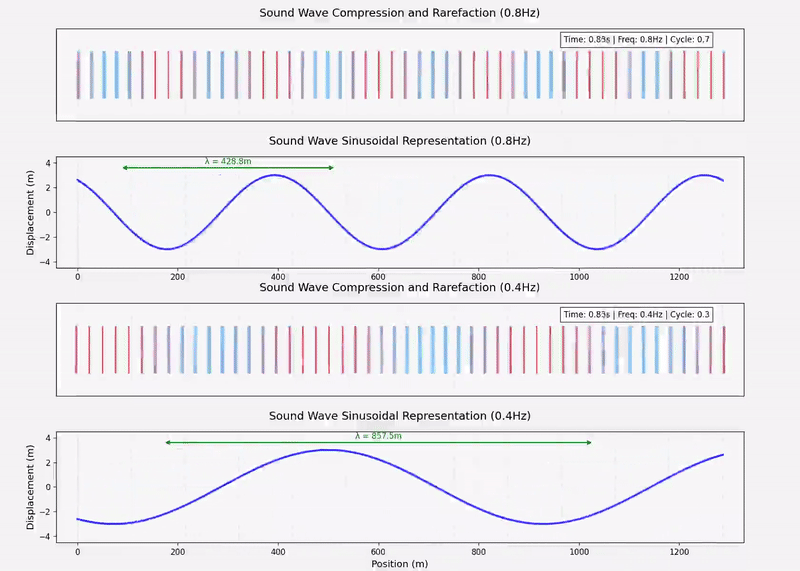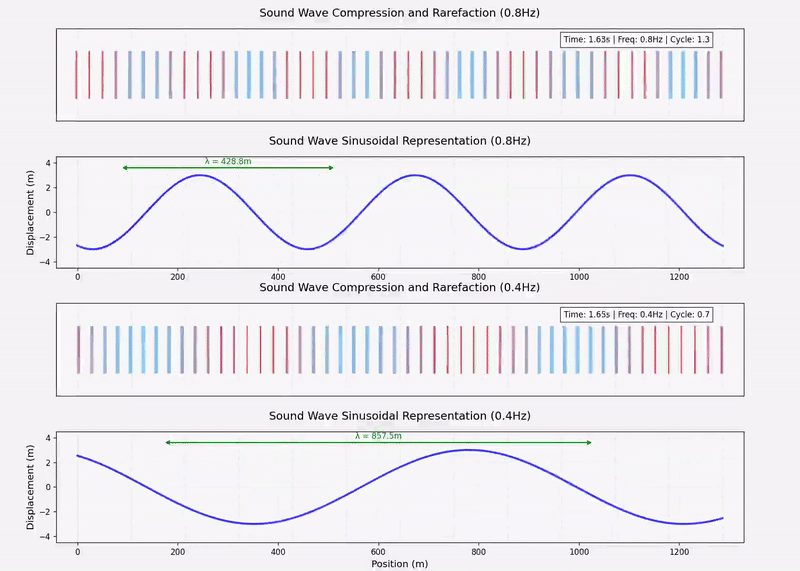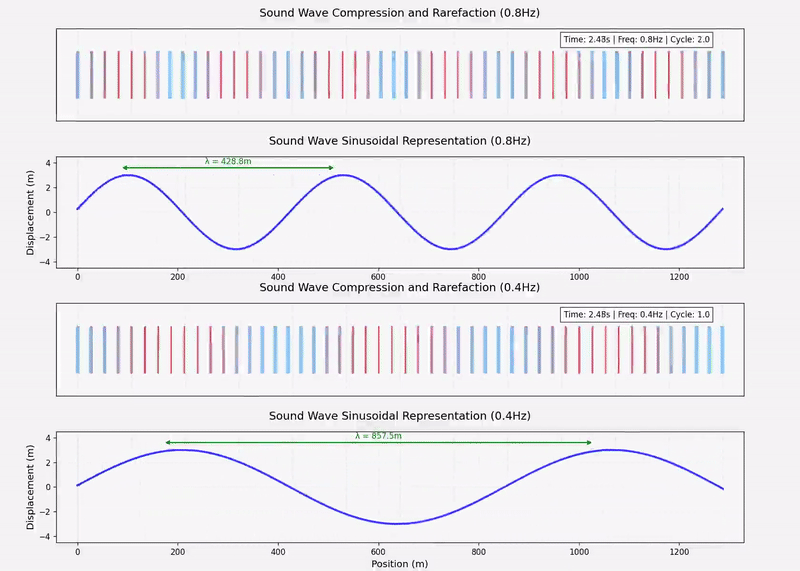
发声物体/乐器的分类
一般乐器主要由三部分组成为耦合振动系统1:
(1)振动体(管、弦、簧、膜、板),这是主要声源;
(2)激发体,用以激发主要声源;
(3)共振体,如共鸣板、空腔,发射声音。
振动体决定基音和泛音的频率,激发体决定激发的大小和频率(主要是基音或某个分音),共振体则给乐器的音色以固有特征。 本文主要目的之一是解释笛子的发声原理,又因弦是常见乐器,所以以下介绍弦和管的振动方程和频率方程。
弦和空气柱的振动方程和振动频率
在简化的一维模型下,弦的振动方程和空气柱的振动方程都是二阶线性齐次偏微分方程,具体推导见参考文献2。
弦
弦的振动方程为
\begin{align} \dfrac{\partial^2 y}{\partial t^2} = c^2 \dfrac{\partial^2 y}{\partial x^2} \end{align}
$y(x,t)$ 是弦在位置 $x$ 和时间 $t$ 的横向位移;$c$ 是波速, $c = \sqrt{T/\mu}$, $T$ 为张力,$\mu$ 为线密度。
经推导,两端固定的弦的振动方程的驻波解为
\begin{align} u(x,t) &= \sum_{n=1}^{\infty} u_n(x,t) \\ &= \sum_{n=1}^{\infty} X_n(x) T_n(t)\\ &= \sum_{n=1}^{\infty} B_n \sin\left( \frac{n\pi x}{L} \right) \cos(\omega_n t - \phi_n) \end{align}
可知弦的总振动是所有可能驻波的叠加。弦发出的声音的频率即弦的振动频率,其角频率为 $ω_n = (n π c) / L$,因此弦的振动频率为
\begin{align} f_n = \frac{\omega_n}{2\pi} = \frac{n c}{2L} = \frac{n}{2L} \sqrt{\frac{T}{\mu}}, \quad n = 1, 2, 3, \dots \end{align}
空气柱
空气柱的振动方程为
\begin{align} \dfrac{\partial^2 \xi}{\partial t^2} = c^2 \dfrac{\partial^2 \xi}{\partial x^2} \end{align}
$ξ(x, t)$ 是空气柱在位置 $x$ 和时间 $t$ 的质点位移。$c$ 是声速,$c = \sqrt{\gamma P_0 / \rho_0}$,$γ$ 为比热容比($\approx 1.4 $), $P_0$ 为平衡气压,$ρ_0$ 为平衡空气密度。
开管空气柱(两端开放),频率方程为
\begin{align} f_n = \frac{n c}{2L}, \quad n = 1, 2, 3, \dots \end{align}
闭管空气柱(一端封闭,一端开放),频率方程为
\begin{align} f_n = \frac{(2n - 1)c}{4L}, \quad n = 1, 2, 3, \dots \end{align}
$L$ 是管长。
开管频率为 $c/(2L)$ 的整数倍,闭管频率为 $c/(4L)$ 的奇数倍。
基音与泛音
$n = 1$ 的频率 $f_1$ 为物体的固有频率,称为基频或基音,$n > 1$ 的各次频率,称为泛频或泛音。$f_1$ 决定音高,不同模态的振幅 $B_n$,或者说 $ f_n = n f_1 $ 确定音色。
感知声音
人体通过感受器官来感知世界,人有五类感官(眼、耳、鼻、舌、身)产生五类感觉(视觉、听觉、嗅觉、味觉、触觉)。人体感知世界的具体机制为:感官器官细胞接受刺激产生神经信号(电信号),神经信号通过神经细胞传至大脑,大脑(通过经验)处理整合,产生感觉。
自然界有许多数量级跨度大的数据,声音的频率也如此。人脑接受这些刺激时,会将跨越数个数量级的数据处理为区间(弱,强)的感觉。
现有两种理论模型用于表示人脑对非线性的数据的处理,分别是韦伯-费希纳定律(Weber-Fechner Law)和史蒂文斯定律(Stevens’ Power Law)。
韦伯-费希纳定律:
\begin{align} P = k \cdot \log\left(\frac{S}{S_0}\right) \end{align}
$P$ 为感知强度,$S$ 为物理刺激量,$S_0$ 为感觉阈限,$k$ 为常数。
史蒂文斯定律:
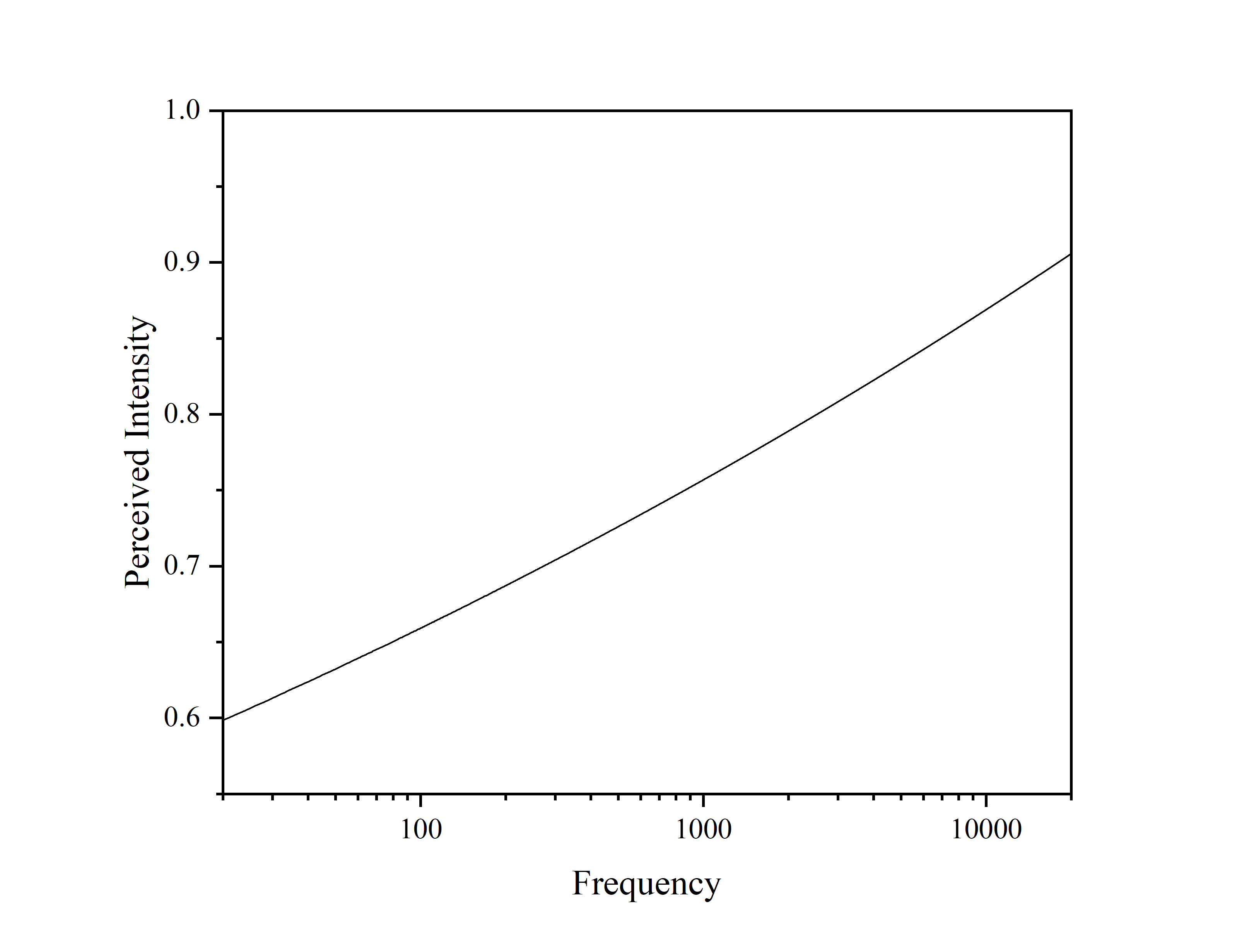
\begin{align} P = a \cdot S^n \end{align}
$P$ 为感知强度,$a$ 为常数,$n$ 为特定感官的指数,对于声音频率 $S = f$,$ n \approx 0.06 $。
在横对数坐标轴画出史蒂文斯定律方程(下图),可描绘感知强度与频率的对应关系。
由图可知,人对声音频率的对数值的感知是近线性的。钢琴上的按键从左到右逐个按下,虽然频率值不是线性递增,但其频率的对数值是线性增加的,所以感觉上音高是线性增加的。
呼吸
人体呼吸按主导的肌肉分类有两种:胸式呼吸和腹式呼吸。
胸式呼吸: 以肋间外肌为主要动力源,收缩时提升肋骨,扩大胸腔横向直径。胸式呼吸浅而短促,通气量较小。
腹式呼吸: 以膈肌(横膈膜) 为主要动力源,收缩时下移压迫腹腔脏器,使腹部向前隆起,肺充分扩张。腹式呼吸深而缓慢,通气量大。
传统上所说“气沉丹田”指的便是腹式呼吸。
进行演唱和管乐器演奏时,常用腹式呼吸。

基础乐理
本章内容参考李重光的《音乐理论基础》。
音
音有高低、强弱、长短、音色等性质,分别对应频率 $f$、振幅 $A$、持续时长和泛音的相对振幅比。一般意义上说的某个音,指的是频率性质。
音律
音律,是规定音的规则系统。人耳能听到的频率范围内有无数音,规定使用哪些音进行音乐创作是有必要的。音律确定各音的关系和基准音。现在,最普遍、使用最广泛的音律为十二平均律。
十二平均律确定各音的方法为:有频率值等比递增序列 $f_{i}, f_{i+1}, f_{i+2}, \dots, f_{i+12}$,其中 $f_{i+12} = 2f_{i}$。得到公比 $r = 2^{1/12}$。确定基准音 $f_i$,则
\begin{align} f_{i+n} = f_i \cdot 2^{n/12},\quad n \in \mathbb{Z} \end{align}
基准音确定为 440 Hz,通过上式,得到十二平均律各音的频率。
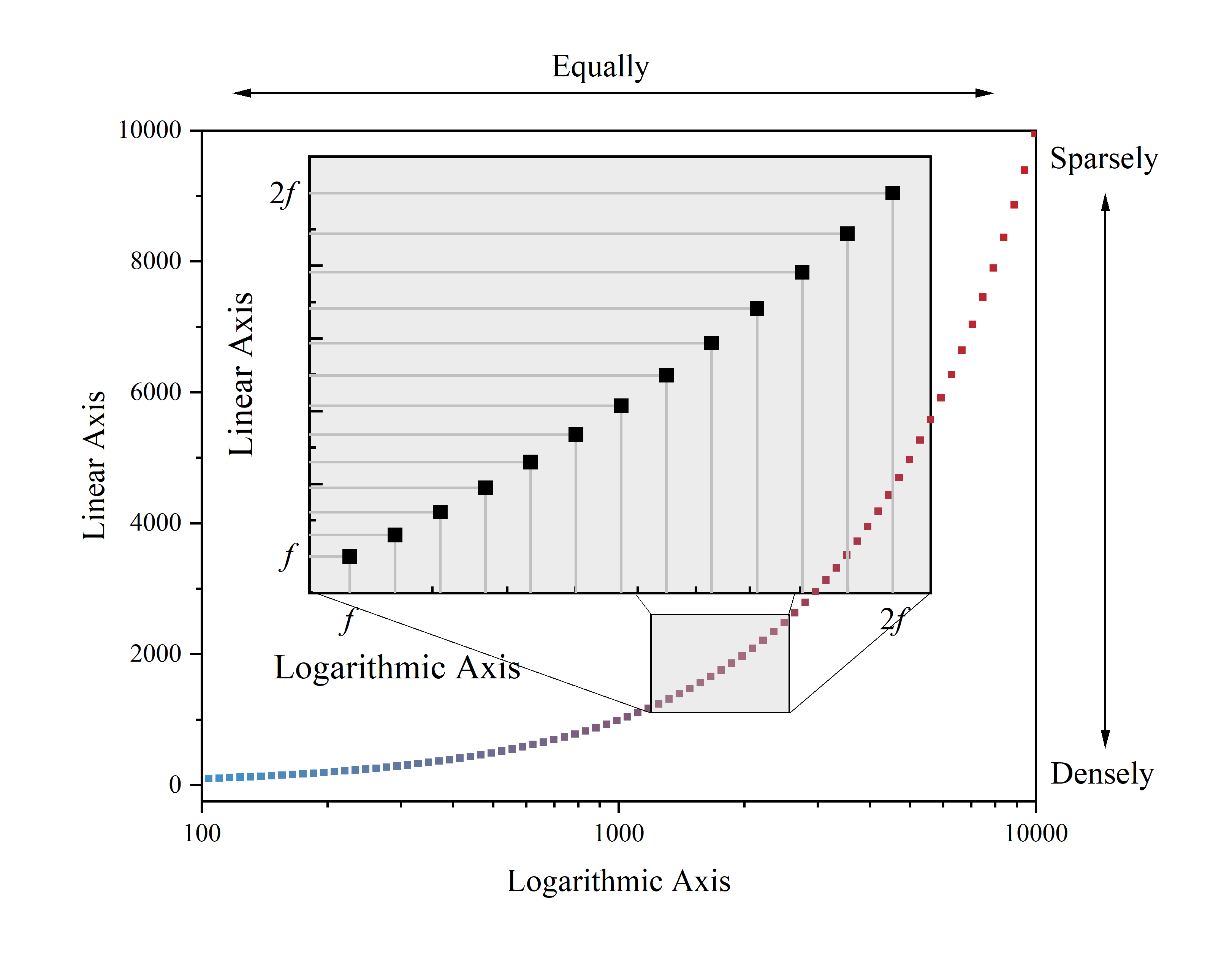
把十二平均律各音的频率值在线性轴和对数轴排列,如图。可以观察到:在线性轴,随频率越高,间距越稀疏;在对数轴,频率间是等距的。
音乐理论,以下按名词简要列出 音、音的关系
WIP
乐律 记谱 五线谱 简谱